 |
Problems
|
Author Tom Hollings : email carmam1536"at"gmail.com
All references are to A. Einstein - "Relativity, The Special
And The General Theory" Methuen and Co. 1920
The theory of relativity as expounded by Einstein gives a very clear
insight into what happens in the real world, especially at extremes of
velocity and/or mass. There are, however, some questions which need
answering.
Three people deserve a mention here. They are Bernard Burchell, who wrote the web page Alternative Physics and rewrote my original version of "8. The Twin Paradox" (which I first put on a science forum) to make it more realistic and more readable. Second is Hans Zweig, who wrote Relativity Unraveled. They have both helped me tremendously. Third is the late Homer Tilton, who very kindly sent me a free copy of two of his and Florentin Smarandache's books "Begin The Adventure" and "Today's Take On Einstein's Relativity".
MENU
1. The Lorentz transformations2. SRT in the Global Positioning System
3. Definition of simultaneity
4. Clocks in motion
5. Clocks and gravity
6. The equality of inertial and gravitational mass
7. The constancy of the velocity of light
8. Speculation on light
9. The twin paradox
10. Experimental evidence on the constancy of the velocity of light
11. Conclusions
12. Appendix
1. THE LORENTZ TRANSFORMATIONS. Ref :- Chapter XI
1A. When Hendrik A. Lorentz devised his transformation
formulae in 1890 he thought that they applied only to electrically
charged bodies, but Einstein incorporated them into his special theory
of relativity assuming that they applied to all bodies. The theory
tells us that with increasing velocity, the mass increases (becoming
infinite at the speed of light, and therefore preventing any further
acceleration), length decreases (length contraction along the line of
motion), and time dilates. All these phenomena occur with respect to
the observer, whom Einstein positioned at the launch point (starting
point). This is important, as an observer placed anywhere other than in
a direct line with the motion of the accelerating body will not measure
the same velocity, but a reduced one, until, when at 90 degrees to the
motion, the relative velocity is zero. Relative velocity is the
measured or calculated velocity between observer and receeding (or
approaching) object. This is the velocity as would be measured by for
example a police radar gun.
This is the equation for mass increase : m' = m / sqrt( 1- ( v / c )^2)
where m' = the calculated mass of the body in motion
m = the rest mass (proper mass)
v = the velocity of the body as seen by the observer
c = the velocity of light
Any body which has been accelerated to an appreciable velocity for the
increase in mass to be tested (and proved?) has been accelerated by an
external force which is itself electro-magnetic and therefore
constrained to the speed of light. These formulae therefore apply only
to bodies which receive an acceleration from an external force, and the
increase in mass and length contraction is with respect only to the
reference frame from where the force originated. The increase in mass
and length contraction are illusions. If an external electro magnetic
force, as in a particle accelerator, is used to accelerate a body, the
electro magnetic field is itself constrained to the speed of light with
respect to the PA, so it cannot possibly accelerate the body past that
speed. The observed effect is as though the body has increased in mass.
Imagine now a space rocket, which is propelled by ejecting a small
amount of matter (the rocket exhaust) at high speed from the rear, so
imparting a thrust in the opposite direction. We will assume that the
exhaust velocity is 3,000 m/s and the mass of the rocket is 30,000 Kg
(very similar to NASA's Mercury-Redstone rockets). Now we can use the
Lorentz transformation to calculate the new mass. As the assumed
velocity
between
exhaust and rocket is 3,000 m/s :-
m' = m / sqrt( 1 - ( v / c )^2)
m' = mass of rocket at velocity v as measured by the essential
observer.
Einstein's observer, properly called the essential observer, is
implicitly always at rest relative to the motive force. In this example
therefore, the essential observer is in the same frame as the rocket
exhaust.
m = 30,000 Kg (proper mass of rocket or rest mass when v = 0)
v = 3,000 m/s - rocket's velocity relative to the exhaust
c = 300,000,000 m/s (rounded up for simplification)
m' = 30000 / sqrt( 1 - (3000 / 3e8)^2) = 30,000.0000015 Kg
The increase in mass is therefore 0.0000015 Kg or 0.0015 gram which is
simply not measurable compared to 30,000 kilograms. For all intents and
purposes the mass increase is zero. A further point to note here is
that the mass increase is measured against the exhaust which is
providing the motive force, and no matter what the velocity of the
rocket when measured against its starting point (or anything else for
that matter), the velocity between rocket and exhaust never changes, so
the rocket's calculated mass m' is always 30,000.0000015 Kg
(disregarding the loss of mass due to fuel used). In other words, the
mass is fixed at
30,000.0000015 Kg for the values used above between rocket and exhaust,
and the extra 0.0000015 Kg is an insignificant amount. As there is no
significant mass increase with velocity, and certainly no accumulative
mass increase, there is no theoretical upper limit to the velocity of
the rocket.
It therefore follows that as the mass increase is virtually zero, m
aproximates very closely to m0. If the acceleration is regulated to 1g
for the comfort of the crew, the space ship can reach an enormous
velocity, and time on this space ship will pass at exactly the same
rate as back at home on earth. "The effects of gravity are
indistinguishable from the effects of acceleration " [AE] (with the
qualification in section 5).
I know that relativists would say that the mass increase has to be
measured relative to the starting point of the rocket, but why is that?
Einstein used the (essential) observer against which to measure the
mass increase, with the tacit assumption that the starting point was
where the propulsion unit was located, as in a particle accelerator.
With that assumption, it is reasonable to refer the mass increase to
the starting point. If we assume the propulsion unit (rocket
motor) is remote from the rocket, then it is perfectly true that the
rocket cannot exceed the speed of the rocket exhaust, as a particle in
a particle accelerator cannot exceed c.
This is analogous to a space vehicle which uses light sails for
propulsion. The sails are deployed in the vicinity of a star (the Sun),
and the light hitting the sails imparts a tiny acceleration away from
the Sun. This acceleration will propel the vehicle away from the Sun,
and the velocity will gradually but steadily increase. As the vehicle
approaches light speed however, the energy from the light striking the
sails gets less and less, and the acceleration gets less and less.
"This
type of propulsion cannot cause the space vehicle to reach or exceed
light speed relative to its source, the Sun."
Quote from "Begin The Adventure" by Homer Tilton and Florentin
Smarandache.
Begin
the Adventure
"A sailing vehicle which depends on light from the sun to accelerate it
remains in that way connnected to the sun, its reference is the sun,
and its speed is limited to less than the speed of light c, relative to
the sun. Propulsive energy cannot reach a vehicle traveling away from
the sun faster than that. It is limited to the speed of light for the
same reason that a cablecar is limited to the speed of the cable
pulling it."
There is another scenario which proves that that faster than
light travel is possible just using logic. The same scenario as
previous is used, ie the space rocket and its rocket engine. The actual
amount of mass which is being ejected from the rear at 3,000 M/s was
not quantified, because there was no need to do so. There is still no
need to accurately quantify it in this new scenario either, as just an
assumption will do. The assumtion is that 3,000 Kg of mass is ejected
from the rear every second. The SRT argument for not surpassing or
reaching light speed is that as the velocity of the rocket increases,
so does its mass, according to the formula :- m' = m / sqrt(1- ( v / c
)^2).
This means that as light speed is approached and the mass increases
towards infinity, the acceleration gets less and less, and when at
lightspeed
the acceleration is zero.
I have used the rocket exhaust velocity with respect to the rocket in
the discussion above to show that by using an internal rocket motor and
using the formula with v representing the velocity between rocket and
exhaust, which never changes from 3,000 M/s, light speed can be
exceeded relative to the starting point. Now it can be shown that by
using the formula from the viewpoint of the starting point or the
external observer, the same conclusion can be reached.
Referring to the formula again, look carefully at what the v
represents. It represents the velocity between the observer and the
space rocket, that is obvious. What is not so obvious however, is that
it also represents the rocket exhaust which is in the same frame as the
rocket. Well actually not quite the same frame, as there is a 3,000 M/s
difference between rocket and exhaust, but this difference is
negligible and amounts to a mass increase of only 0.0000015 Kg, which
is a fixed amount for the fixed 3,000 M/s exhaust velocity. Therefore,
as the rocket mass increases, the exhaust mass increases in unison. The
mass ratio rocket to rocket exhaust stays the same, no matter what the
velocity is with respect to the external observer. As the force stays
the same pro rata, the velocity steadily increases, and the rocket can
surpass lightspeed WRT the observer or starting point. Of course the
observer will lose sight of the rocket as it passes light speed.
************************************************
1B The passing rocket.
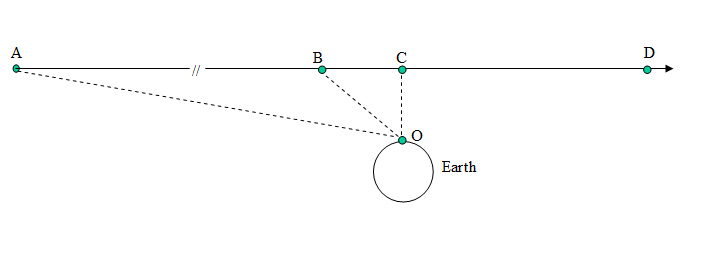
A D is the arbitrarily long path of a rocket passing Earth with a
velocity relative to that line of 100,000 kph. When the rocket is at
point A the relative velocity along the line A O to the observer
(assume a GPS receiver to tie in with later paragraphs) at point O is
very slightly less than 100,000 kph due to the shallow angle C A O, but
if the distance A C is many times larger than the distance C O, this
difference in velocity is negligible and the relative velocity can be
assumed without error to be 100,000 kph. Point B is 25,000 Km from
point C and point O is also 25,000 Km from point C. When the rocket is
at point B the difference in the relative velocity which is now along
the line B O is not negligible and is 70,710 kph due to the angle C B O
being 45 degrees. When at point C the relative velocity is zero because
the rocket is no longer approaching point O. The same effect happens in
reverse going from C to D.
Mathematically, that is :- The vertical distance is OC, the
horizontal distance is BC, and the rocket velocity is v.
The horizontal distance based on a function of time t is BC -v*t.
The rocket is at B when t = 0 .
Using Pythagoras, the distance BO is :-
Distance BO = sqrt(OC^2 + (BC-v*t)^2)
Velocity BO = the time deritive dx/dt = -v*(BC-v*t) / sqrt(OC^2 +
(BC-v*t)^2)
At t = 0 that is -v*BC / sqrt(OC^2 + BC^2)
Substituting CO = BC = 500,000 and v = 100,000
= -100,000/sqrt(2) = -70,710 kph (negative as it is the velocity
towards O)
This raises a very valid point. The SRT time dilation between a GPS
satellite in orbit and a GPS receiver on Earth is based on the
satellite's orbital speed when it should be based on the relative
velocity between the satellite and the GPS receiver. It can be seen
from the diagram above that the rocket at position C is equivalent to
the satellite in orbit when at that same point, so there is no relative
velocity between points C and O. In other words, when the satellite is
directly overhead the GPS receiver there is no relative velocity beween
them.
Here is the SRT formula for time dilation :- t' = t / sqrt(1- ( v / c )^2) .
Question. What does the v refer to in the formula? Answer. It refers to the velocity between the two frames involved (F1 and F2).
Examples. In Einstein’s light clock thought experiment, the clock is in F1 with the observer in F2, and v is the velocity between them (as everything is reciprocal, the frames are arbitrarily numbered and could be the other way round). The v is therefore the velocity between F1 and F2 as would be measured by for instance a police radar speed gun which always measures the speed in a straight line between the gun and the vehicle (IE the relative velocity).
In the case of a rocket launched from Earth and travelling away in a straight line, and we want to use the formula to find the time difference between Earth and rocket, the two frames are the Earth and the rocket (F1 and F2), and the velocity between them is v (this is the only example where one of the frames is the Earth itself).
In the case of two rockets (F1 and F2) which are in deep space travelling at different speeds and we want to find the time difference between them, v refers to the velocity between them, and Earth does not come into the calculations.
In the case of two (extremely fast) cars on a long straight road here on Earth, it refers to the velocity between the two cars (F1 and F2), and here also Earth does not come into the calculations.
Now we move to a GPS satellite in orbit, and a point on the Earth which could be stationary or moving - e.g. a car, and the two frames now are the satellite and the car, which are F1 and F2 (one car and one satellite are used in this example to simplify the situation), and again Earth does not come into the calculations. The v always refers to the velocity between F1 and F2, and no other frames are relevant. We will assume that the car is stationary on the Earth and the GPS satellite is moving in its orbit at approximately 4,000 M/s. Note that this orbital speed is not a velocity, as the GPS satellite's orbit is a near circle (the eccentricity is actually less than 0.02) around the Earth, and the velocity v in the formula is in a straight line between car and GPS satellite. The GPS satellite is orbiting the Earth at a height of 20,200 Km, so it is never getting any closer to or further away from the Earth’s surface, and stays permanently at that height above it. It should now be obvious that 4,000 M/s is not the velocity between the GPS satellite and the car, and yet in the formula for time dilation t' = t /sqrt(1- ( v / c )^2) between the GPS satellite and the car, v is set to 4,000 M/s.
So what is the measured or calculated velocity between the GPS satellite and the car? That depends on the position of the satellite in its orbit. When the satellite is directly over the car, the velocity v is zero, because it is neither approaching nor receding from the car. If a line were to be projected vertically upwards from the car to intersect the satellite’s orbit, the intersection angle would be 90 degrees and there would be no motion along that vertical line by either the car or the satellite, so a radar gun (which always shows relative velocity) would show zero velocity along that line. As the satellite moves in its orbit away from overhead as viewed from the car, it moves down towards the horizon. On its way down, it is moving away from the car. When the satellite is directly overhead, its distance from the car is 20,200 Km, but when at the horizon the distance is 25,700 Km. Therefore the velocity between the two increases from zero when overhead, until when at the horizon it is apx +928 M/s. When the satellite is on its way up on the other side it is moving towards the car and the relative velocity is decreasing from apx -928 M/s until overhead the car again when the velocity is zero once more.
The velocity which should be used as v is therefore constantly
changing.
Now take into account the fact that there are multiple GPS users and
satellites. That change in velocity is different for every car (GPS
receiver) and every satellite (transmitter), and cannot be accounted
for because the same data from one satellite is received by more than
one GPS user and one GPS user is receiving data from more than one
satellite, and all users and satellites can be moving at different
speeds and in different directions.
The GPS designers use the orbital speed of the satellite for v, even though it has absolutely no relevance to the velocity between satellite and car or in fact any relevance to any point on Earth.
The question which must be asked (and answered) is : - "Why is the satellite's orbital speed used for v?"
Your comments would be appreciated :- email :- carmam1536"at"gmail.com
3. DEFINITION OF SIMULTANEITY. Ref :- Chapter IX.
Einstein uses lightning strikes at two places on the
railway track, and
says that although they can be said to be simultaneous as judged from
the embankment at a vantage point exactly equidistant from them, when
judged from the moving train, they are not. He uses this as an argument
for there being a different time in moving frames of reference.
I have difficulty in accepting this argument for the following reasons.
In judging whether the lightning strikes are simultaneous, he uses
light itself as a medium for carrying the information to the observer,
without making any correction for the known finite velocity of light.
Any number of other observers on the embankment, who are position so as
not to be equidistant from the two lightning strikes, see the same two
lightning strikes, but do not observe them to be simultaneous, and
indeed,
observe the timing difference between them to vary depending on where
on the frame they are. This leads us to the conclusion that there can
be an infinite number of time scales within one frame of reference - a
conclusion which is not in accord with reality.
Also, we could, with equal validity, have visualised two workmen with
hammers, and used sound to convey the information to the observer. The
results then achieved would be markedly different from those using
light, but nonetheless would be perfectly valid. Of course you point
out that we should use the fastest medium that we can - which is light.
Yes - use it by all means, but acknowledge the fact that it has a
finite velocity and compensate for it. To get accurate results we
should be using as a medium something which carries the information
instantaneously - but we know of no such medium. If we postulate the
existence of such a medium, and use it in a thought experiment, two
occurrences judged to be simultaneous from the embankment (wherever the
observer is positioned) will also be judged to be simultaneous from the
moving train.
Chapter IX, paragraph 2 states "Are two events ... which are
simultaneous with reference to the railway embankment also simultaneous
relative to the train? We shall show directly that the answer must be
in the negative."
"Events which are simultaneous with reference to the embankment are not
simultaneous with respect to the train, and vice versa." (relativity of
simultaneity).
Let us put our trust in the able meteorologist, and
position ourselves on the embankment exactly equidistant (at point M)
from the two lightning strokes A and B. An observer in the speeding
train at position M* is exactly at position M on the embankment when
the lightning strokes occur, but as he is speeding towards B, and away
from A, he sees the flash from B before he sees the flash from A, and
assumes them to be not simultaneous. If I now tell him the velocity of
light, the velocity of his train, and the distance M to A (which is the
same as M to B), he can easily work out the distance that he has
travelled and the distance that the light has travelled. This will tell
him that the lightning strokes were in fact simultaneous."
The inference from this discussion is that when the velocity of light
is taken into account and compensated for, an occurrence judged to be
simultaneous in one frame is also simultaneous in another. Einstein
uses this definition of simultaneity to determine that one reference
frame has a different time scale to another which is in (non
accelerated) motion relative to it, but when the velocity of light is
properly compensated for, there is no need for different time scales,
and absolute time can be used throughout all reference frames, whatever
their (non accelerated) motion. This however, comes into conflict with
the assumption that the velocity of light is the same in all reference
frames, which is discussed in section 8.
4. CLOCKS IN MOTION. Ref :- Chapter XII
Most physics books use a light clock in their proof
of the time
dilation effect, one "tick" of the clock being the time it takes a
pulse of light to travel from the source to a mirror and back. When the
pulse arrives back at the source, the electronics ensures that another
pulse is initiated, ad infinitum. The observer O also sees the pulses
of light as they are initiated.
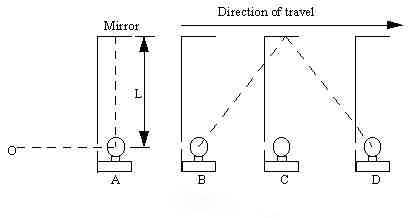
In A the clock is at rest relative to the observer (both are in
reference frame F1), and the light pulse travels the dotted path to the
mirror and back in T = 2L/c. In B to D, the clock is moving (now in
reference frame F2) relative to the observer who is still in F1, and he
sees that the pulse has further to travel - hence the time dilation.
When the clock is in motion relative to the observer in F1, the
observer sees the clock running slow according to the Lorentz equation
:-
T' = T / sqrt(1 - (v/c)^2)
This time dilation depends on the velocity of light being the
same for all observers. On page 37, we can read this :-
"As judged from K, the clock is moving with velocity v; as judged from
this reference body, the time which elapses between two strokes of the
clock is not one second, but 1 / sqrt(1 - (v/c)^2) seconds, ie a
somewhat larger time. As a consequence of its motion the clock goes
more slowly than when at rest. Here also the velocity c plays the part
of an unattainable limiting velocity."
Note those very misleading last two sentences. The impression is given
that the clock is actually running slow, not just judged to be running
slow. The unattainable limiting velocity is just as judged from K, and
not physically unattainable.
Remember that the above discussion depends on the velocity of light
being the same for all observers. This has not been proved, only
inferred. For a detailed discussion on light, go to Alternativephysics/light.
This is an excellent web page by Bernard Burchell.
Let us put the clock far out in space, so there is no
reference point as to its velocity, or equivalently, imagine the clock
to be alone in the universe. Let us further imagine that it is in a
perfect vacuum. In line with the discussion in section 8 of this paper
about what
constitutes a vacuum, I shall define a perfect vacuum as there being no
atoms whatever in the path of the light beam, no matter what the
velocity of the clock or its position in space. Now we have absolutely
no way of knowing whether it is in motion or not. We are in F1, measure
the clock's rate, and find one tick to be T = 2L/c. The light pulse
has travelled the path as in A. Now a force of 1G is applied for 4,252
hours, so the clock is accelerated, and then the force removed. The
clock must now be at half the speed of light relative to its velocity
during the first measurement of its rate, but of course there are no
reference points, so there is no way of knowing this. The rate of the
clock is measured, and found to be T = 2L/c. In a vacuum, in its own
reference frame, the rate of the clock does not alter.
This paragraph agrees with Einstein, but the next paragraph is in
conflict with Einstein.
Now the same experiment is done in a medium, which could be air. We
will neglect the fact that air resistance will stop us reaching high
velocities. The observer in the clock's reference frame notes that he
is stationary with respect to the air, and checks the clock's rate,
which he finds to be T = 2L/(c/n). The air then starts to move (in
other words the wind starts to blow, and it blows at half the speed of
light), the observer again measures the rate of the clock (he is
stationary with respect to the ground, but he is standing in a rather
strong wind). He finds that the clock is running slow, as shown in
Fig.2 B to D, according to the equation :-
T' = T / sqrt( 1 - v^2 / ( c / n )^2)
The index of refraction of the medium is n.
The conclusion is that in a medium, where that medium can flow
unimpeded through the path of the light pulse, moving clocks can go
slow, even within their own frame of reference. If the clock's
physical frame impedes the flow of the medium, and slows it down to a
value which is less than its value away from the physical frame, the
clock will not run as slow. If the clock is completely enclosed, e.g.
in an enclosed vehicle which is travelling at half the speed of light,
the enclosed medium is also travelling at that speed, and the clock's
rate is T = 2L/(c/n). Popular teaching states that all clocks run slow
when in motion relative to the observer. What we have just discovered
is that when in a medium, a clock does run slow at velocity, even in
its own reference frame.
A very important point to note here is that the time dilation is caused by the light pulse changing direction through 90 degrees, so it is then transverse to the line of motion. If the light clock itself is rotated 90 degrees clockwise so there is no change of direction of the light pulse, the observer will not see any time dilation. This completely nulifies any argument that this light clock provides "proof" of time dilation.
5. CLOCKS AND GRAVITY.
Part A.
Let us expand on the discussion about clocks.
When Einstein published his paper The General Theory of Relativity in
1915, one of the things that it predicted was that gravity affects
time. The lower the gravity, the faster time flows, the higher the
gravity, the slower it flows. It would appear that this prediction has
been proved correct, but has it?
There is another school of thought, and one which I subscribe to. Time
is not running faster in lower gravity (ie at the top of a mountain as
in a popular example), it is quite simply the clock which is running
faster.
Here is a thought experiment which proves my point, and it could be
very easily (but not cheaply) performed in actuality.
Place an atomic clock on the Moon alongside a pendulum clock. A
pendulum clock keeps time according to the formula P = 2π * √(L/g).
The only two (major) variables are the length of the pendulum (L) and
gravity
(g = 9.83 m/s^2 here on Earth, and 1.62 m/s^2 on the Moon). The gravity
on the Moon is 1/6 of that on Earth, so a pendulum clock with
a pendulum length of 0.1 meter (100mm) would run at one complete
oscillation of the pendulum in 0.6340 seconds here on Earth, but on the
Moon it would take 1.5607 seconds. The atomic clock is affected to a
far lesser extent. Over one year, the Moon atomic clock would run
faster than the Earth atomic clock by 0.02 seconds per year, a trifling
amount which can be ignored in this discusion. Here are the maths for
those interested.
P = period of pendulum = 2 * pi * sqrt( L / g )
L = length of pendulum
g = gravitation force
Earth : P = 2 * 3.1416 * sqrt( 0.1 / 9.83) = 6.2832 * sqrt(0.0102) =
6.2832 * 0.1009 = 0.6340 seconds
Moon : P = 2 * 3.1416 * sqrt( 0.1 / 1.62) = 6.2832 * sqrt(0.6170) =
6.2832 * 0.2484 = 1.5607 seconds
While the atomic clock on the Moon counts 2.46 seconds, the pendulum
clock would count one second. This of course is assuming that all other
factors are the same, probably the most important being temperature (a
minor variable),
but even a large temperature change would be nowhere near the effect of
the gravity change. For example, if the temperature of the pendulum is
increased by 300 degrees centigrade, which is quite possible moving
from shade to
direct sunlight on the Moon, its length would increase by around 0.3%,
and the period would increase by a small amount.
Moon at nominal+300 degrees C :
P = 2 * 3.1416 * sqrt( 0.1003 / 1.62) = 6.2832 * sqrt(0.0619) = 6.2832
* 0.2488 = 1.563 seconds
The heat effect is negligible in comparison to the gravity effect.
As stated above, because of the reduced gravity, the atomic
clock will
run faster on the Moon than the Earth by around 0.02 seconds per year.
As this experiment is confined to the Moon, there is no need to take
into account any SRT time dilation as seen from Earth. If Einstein is
correct, and it is time itself which has speeded up, the pendulum clock
will speed up and agree with the atomic clock. This claim is absurd, as
the pendulum clock will run as defined by gravity and pendulum length
alone, so the two clocks will disagree.
Which clock is correct? The answer is neither is correct because they
have been calibrated on Earth. Gravity is affecting the rate of both
clocks, not altering the passage of time. The atomic clock is of course
affected by gravity to a far less extent than the pendulum clock, and
in the opposite sense. The pendulum length of 100mm has been chosen as
a clock this size can easily be stowed on the Moon lander and kept in a
shock proof container until the lander is on the Moon. It can also be
left in the lander shielded from direct sunlight for the duration of
the experiment. Also, the duration needed to notice the difference in
timekeeping is very short. After 2 minutes and 27 seconds acccording to
the atomic clock, the pendulum clock is reading one minute, so the
experiment can be re-run many times while the lander is on the Moon.
I am here assuming that the Moon lander has an atomic clock on board,
but have not been able to find any firm evidence if this is the case.
Due to the large difference in the timing, a simple wristwatch would do
the job very adequately, as the wristwatch is not affected by gravity,
and will run at the same rate on the Moon as here on Earth.
Part B.
The following section is reproduced here from Doug Marett's exellent Conspiracy of Light with his kind permission :-
The simplest time dilation effect to test is gravitational time dilation, the speeding up of clocks with altitude. According to Einstein, the rate of time follows the gravitational potential, so a clock on the surface of the earth should count more slowly than a clock at some high altitude, such as at the top of a mountain. Time is alleged to be moving into the future faster at the top of a mountain. So we need a clock on the Earth that is unaffected by altitude. Let's say we use the rotation of the earth as our clock instead of a conventional cesium clock. After all, our human concept of time, and the units that compose it (days, hours, minutes, seconds) are already derived from the rotation period of the earth, so it should be the ideal clock for comparison. For each observer, we could use as our reference the position of the sun in the sky, or the position of a Foucault pendulum, or most preferably the position of the fixed stars in sidereal time. If we measure the sidereal day (23.93447 hours) as the time for one earth rotation relative to the vernal equinox, using a sighting star as a reference, we can then place an observer A at the top of a mountain, and another observer B at sea level. Preferably the mountain observer is exactly vertical over the sea level observer, and this vertical line passes through the center of the earth. We use as our example the mountain Pico del Teide on Tenerife, with an altitude of 3718 meters. We give each observer A and B a cesium clock, and a sidereal clock.The sidereal clocks mark a tick when the reference star is directly overhead each day. The cesium clocks mark a tick when 23.93477 hours has passed in their local time. We then compare the four clocks to determine if they are counting at the same rate. What happens is that when the reference star passes over observer A and B, both sidereal clocks trigger at the same moment, differing only in the light propagation time between A and B. Because this propagation time is a fixed amount, it does not affect the rate at which the two clocks count – therefore the count rate is exactly the same. However, since both cesium clocks experience gravitational time dilation, the cesium clock at observer A must count faster than the cesium clock at observer B. If we had pre-synchronized the two clocks at sea level, then the cesium clock at observer A will begin to go out of synchronization with the other three clocks, and the amount of time gained by cesium clock A will continue to increase as the days pass. Clearly three of the 4 clocks agree on the amount of elapsed time – only cesium clock A reads in error. The fact that we have created clocks immune to time dilation implies that real time has never changed at the top of the mountain – apparent time dilation is an artifact of the difference in the speed of light at two difference points in space, and the use of clocks calibrated to the speed of light – i.e. the light clocks of Einstein.
This conclusion is also consistent with our reason – given the millions of years that the mountain has been around, the summit of Pico del Teide should by now be several minutes in the future compared to the land at its sea shore base. And yet they are physically connected. To believe that time dilation is real would require us to assume that walking up the mountain is the same as walking into the future - the land would have to form a bridge between two points in Einstein’s dimension of time. It is somewhat trivial to travel to the top of the mountain and view through a telescope a clock tower in Puerto de la Cruz far below to verify that the top of the mountain and the sea side resort share the same present.
6. THE EQUALITY OF INERTIAL AND GRAVITATIONAL MASS. Ref :- Chapter XX
In chapter XIX Einstein makes the following statement :-
"Bodies which are moving under the sole influence of a gravitational
field receive an acceleration, which does not in the least depend on
the material or the physical state of the body. For instance, a piece
of lead and a piece of wood fall in exactly the same manner in a
gravitational field (in vacuo) when they start off from rest or with
the same initial velocity."
When watching a piece of lead and a piece of wood fall on Earth, they
appear to
fall in exactly the same manner. They do not. The lead actually falls
faster, but the difference in acceleration is so minute that it cannot
easily be measured, and can be completely ignored under all but very
extreme
circumstances.
The Equivalence Principle (chapter XX) states "It is not possible by
experiment to distinguish between an accelerating frame and an inertial
frame in a suitably chosen gravitational potential, provided that the
observations take place in a small region of space and time".
Einstein states (chapter XX) that all objects when dropped, will fall
to the floor with equal acceleration, whether the chest is in a
gravitational field or is being accelerated by an outside force. We are
now in a position to show that this is not the case. Appearances can be
deceptive. We will assume that we are standing on the surface of the
Earth. If you picture a mass the equivalent of the Earth, but
compressed to a size similar to that of the wood or lead under
discussion (it is immaterial what this mass is, but it might be
convenient to picture a miniature black hole), and hold it suspended by
some means, when that mass is dropped, the observed acceleration will
not be 9.8m/s^2, but 19.6m/s^2 . As the Earth's gravity is the
former
value, and as is that of the miniature black hole, we can immediately
see that the gravitational attraction is a result of the attraction of
the two bodies' gravitational fields. This applies whatever the mass
of the bodies, and explains why the wood and the lead appear to behave
the same - their mass is so tiny compared to that of the Earth, that
for all practical purposes when dealing with the Earth, they are
identical in mass.
Referring to Einstein's book again, if the man in the chest is being
accelerated at 1G by an outside force (the hypothetical being pulling
on the rope, or a reaction motor etc) and drops a piece of lead or a
miniature black hole, they will both fall with an acceleration of
exactly 9.8m/s^2 - not a hair under or over. The objects are quite
simply left behind as the chest accelerates away, and will hit the
floor of the chest after 2 seconds if they are at a height of 20 meters
to start with. [experiment 1].
Let us now assume that he is in the gravitational field of the Earth
with the floor of the chest standing on the surface of the Earth. The
objects are again at a height of 20 meters, so that at 9.8m/s^2
acceleration, they would take 2s to hit the floor. The piece of lead
does indeed fall at that rate, but the miniature black hole falls at
19.6 m/s^2 (actually the miniature black hole and the Earth will each
fall towards each other with an acceleration of 9.8m/s^2 each, giving a
total acceleration of 19.6 m/s^2), and hits the floor after 1.4s .
[experiment 2]
To summarise then, if the experiment is done in the accelerated chest,
the objects will hit the floor after 2s. If the experiment is done on
the Earth, the black hole will hit the floor after 1.4s, while the lead
will hit the floor after 2s. He can immediately decide from this
experiment whether he is in a gravitational field or is being
accelerated by an outside force. If a black hole with a mass the same
as that of the Earth falls faster than a piece of lead, then so does a
mass of half the Earth, as does a mass of one hundredth, or a
thousandth etc. In principle, if the man's instruments are sensitive
enough, he can detect whether he is in a gravitational field or being
accelerated, whatever the mass of the objects which he drops.
When watching a piece of lead and a piece of wood fall on Earth, they
appear to fall in exactly the same manner. They do not. The lead
actually falls faster, but the difference in acceleration is so minute
that it
cannot easily be measured, and can be ignored for all practical
purposes.
Is it possible that Einstein did not know this? When Johannes Kepler
wrote his equations for planetary orbital motion in the early part of
the 17th century, he used the masses of both the primary and secondary
bodies, so he knew they had to be additive.
Objections.
Some are rather specious, like saying that a miniature black
hole would
have gravity gradient effects. Yes it would. That in itself proves that
gravity and acceleration are different. The objection I liked most
however was that if I was correct, then a heavy satellite would orbit
faster than a lighter one (in the same orbit) . Yes, absolutely
correct. But, as above, the effect is far too small to be noticed. This
got me to wondering just how large (massive) a satellite would have to
be for this effect to be noticed, which in turn led to a rather
unexpected conclusion.
Here is the scenario, and although a satellite has not been put into
orbit at the stated distance, there is no reason why it cannot be, so
in that respect, it is real. I am going to put a satellite into a
specific orbit and calculate its orbital period and velocity. I will
then calculate the orbital period and velocity of a heavier satellite
in the same orbit.
The orbits are assumed to be circular.
The units used are Kilograms, meters, and seconds. The orbital distance
is 384,900,000m from the centre of the earth. The formula used to
determine the satellite's period (Ps) is :-
Ps = 2 * pi * sqrt( R^3 / G * ( Me + Ms ))
Where R = distance to satellite from the centre of the Earth (or to be
more precise from the centre of mass of the earth satellite system) ie
orbit radius = 384,900,000m
G = the gravitational constant = 6.674e-11
Me = the mass of the Earth = 5.97219e24 Kg
Mm = the mass of the Moon = 7.34767e22 Kg
Ms = the mass of the satellite (for a man made satellite not normally
taken into account, here it is assumed to be 1,000 Kg)
I used Fortran to create a program to calculate orbital velocities from
various orbits and masses. The results from using a calculator may not
be an exact match but will be close enough. The program is available
here for you to check and experiment with, but it
treats the masses as point sources, so will not be accurate with a low
radius orbit around a large mass :-
http://problemswithrelativity.com/sat11.exe
The source code is here :-
http://problemswithrelativity.com/sat11.f95
Ps = 6.2831853 * sqrt( 384,900,000^3 / 6.67e-11 * (5.97219e24 + 1,000))
= 27.51428811520548 days.
For a satellite of 1,000,000,000 Kg (1 billion Kg) the period (in
seconds) is the same
to 9 decimal places. It can now be seen why the mass of a man made
satellite is not normally taken into account when calculating orbital
velocity, as increasing the mass a millionfold will result in an
orbital period difference of 2e-10 seconds in 27.5 days.
The circumference of the orbit is :-
C = 2 pi R = 6.2831853 * 384,900,000 = 2,418,398,092.031479 m
Therefore the velocity of the satellite is :-
Vs = C / Ps = 2,419,371,395.58 / 2,378,191.224559946
= 1,017.31573486328125 m/s
The orbital radius used above is the radius of the Moon's orbit so now
its period is calculated :-
Pm = period of orbit of the Moon.
Mm = mass of the Moon = 7.347673e22 Kg
Pm = 2 * pi sqrt( R^3 / G * ( Me + Mm ))
= 6.2831853 * sqrt(384,900,000^3 / 6.67e-11 * (5.97219e24 + 7.34767e22))
= 2,362,744.336301510490677977736859628 seconds
= 27.346577966452667 days
The circumference of the Moon's orbit is the same as the satellite's
(but not concentric with it, as the two barycentres are different) :- C
= 2,418,398,092.031479 m
The velocity is :-
V = C / Pm = 2,418,398,092.031479 /
2,362,7744.36301510490677977736859628
= 1023.5547 m/s
The Moon is faster than the man made satellite by 6.23895263671875 m/s,
and if the satellite was on the opposite side of the Earth from the
Moon when it went into orbit, the Moon would gradually
catch up with it until they collided. This would take about 6 years.
This treatise is simplified by ignoring any pertubation caused by
passing through the Lagrangian points.
Using the programme, put the Earth into the same orbit as Jupiter, you
will see that they collide in about 12,000 years.
Here is the unexpected conclusion which has emerged: No trinary star
systems will be found in the universe. I define a trinary system as 1)
a system in which the central more massive body has two other bodies in
orbit around it in the same plane and which are nearly equal in orbital
radius, or 2) where there are three bodies orbiting around their common
centre of mass.
If a star system such as 1) formed in the first place, the two stars
which were similar in mass but less massive than the primary would
collide to form a binary system: or if 2) the triangle formed by the
three stars was equilateral (possible but not probable), due to the
differing velocities this triangle would shift to be non equilateral
(this would seem to be a more probable starting point, and is similar
to system 1), and then the two closest stars would approach and
collide. As they did so, a binary system would form. A trinary system
can only exist for a very short time relative to the age of the
universe, and could only be found in very young star systems.
The calculations above show that a trinary star system is not stable.
As can be seen from the above, because satellites of differing masses
in the same orbit move at different speeds, there will be no
trinary systems in the universe, except perhaps in very young star
systems, which will not last long before they collapse.
7. THE CONSTANCY OF THE VELOCITY OF LIGHT
Because of the principle of relativity,
light ought
to have the same
velocity, no matter which frame of reference we are in. Various
measurements have been made by eminent physicists who have come to the
conclusion that the velocity of light is the same in all frames of
reference.
This statement appears to hold true, as the velocity of light has been
measured in various frames of reference which are in uniform
translation with respect to each other. To put this succinctly, if the
velocity of light is measured from a certain star which is at rest
relative to us, it is found to be (simplified by rounding up) 300,000
Kilometers per second (Km/s). If the same experiment is done with a
star which is approaching us at 1,000 Km/s, it might be thought that
the velocity of light would be measured at 301,000 Km/s. This is not
the case, the velocity of light is still measured at 300,000 Km/s. This
difficulty led Einstein to his theory of time dilation. Chapters VIII
and IX.
There are however, two snags. The first is that whatever the speed of
approach or recession, when the star's light reaches our atmosphere,
it slows down, and assumes the velocity for the atmosphere's index of
refraction. The velocity of light in our atmosphere is not c, but a
smaller value which is c/n, where n is the index of refraction of the
"standard" atmosphere. c/n = c/1.00029 =
299,900,000m/s approximately. The second is the rather arbitrary use of
the word vacuum. Einstein made great importance of being precise in his
terminology, so there could be no mis-understanding, and yet a vacuum
is not defined. The very terms solid, liquid, and gas, are themselves
rather arbitrary, and depend on temperature and pressure, so what
exactly is a vacuum? Is it one atom per cubic millimeter on average? Is
it one atom per cubic centimeter? Is it one atom per cubic meter? Space
is not a pure vacuum, it is full of dust and other particles, and this
makes
it a very rarefied gas with its own index of refraction. In fact, in
interstellar space, the density is an average of 1 atom per 10
centimeters, while in the vicinity of the Sun, the density is much
higher at about 1 atom per centimeter. Light therefore travels through
space as it travels through any other medium, at a speed of c/n
relative to that medium. The Michelson-Morley experiment is often
quoted as proving the
constancy of the velocity of light, but it was set up to look for (or
more correctly, to prove, an aether drift). The light source and the
observer were stationary with respect to each other, and the experiment
was done on the surface of the Earth, so how could this experiment
prove whether c is constant with respect to the source or the observer
or both or neither? The way the Michelson-Morley experiment was set up
is akin to trying to find the windspeed by setting up an anemometer in
a closed room. The anemometer has to be outdoors, and the further away
from any obstacles, the more accurate the reading will be. An
experiment to prove the one way
velocity of light has never been done, and it is probably impossible to
do one. It has therefore only been inferred and
never proven directly.
There is an "aether", but not one in the classical sense, and that is
why the Michelson-Morley experiment could not detect it. That
experiment was done on Earth where the speed of light is c/n relative
to the Earth (or more precisely to the atmosphere), whatever its
direction or the direction of the Earth. Let
us move the Michelson-Morley experiment into space, and in fact well
away from the Earth. We will put it on an interplanetary probe, and on
an extension arm some distance from the probe body. Do the experiment
well away from any planet or other large body, aligned with one arm on
a line pointing to the Sun, and the other arm will then be at right
angles to the Sun. One arm is now at right angles to the aether drift
and one arm is aligned with it. The result of the experiment will be an
aether drift towards the Sun. What has been measured here is the dark
matter (DM), and this re-enforces what we already know, that space is
not entirely empty, there are particles moving about through all of
space. In the region of stars, this DM moves towards them, whilst in a
region devoid of stars, it could assume any direction.
The speed of light then is with respect to this "aether", and it has an
index of refraction just the same as any other medium, but this medium
is rather sparse and very fluid, and if taken over a large enough
distance, the currents will cancel themselves out, leaving the speed of
light as c/n relative to the "aether". c/n is of course 300,000,000m/s
or what is commonly known as c.
8. SPECULATION ON LIGHT.
On the Nature of Light. Light has mass. In a thought experiment,
Einstein "proves" that light has mass. This seems to be borne out by
the observation of the bending of starlight near the limb of the sun,
as seen during a solar eclipse. The thought experiment is described as
this :-
Exp 1. A light source (S) with a narrow beam, such as a laser, in a
lift (elevator) at 1 meter high from the lift floor is flashed on when
the lift is stationary. The beam hits the opposite side of the lift at
1 meter height where there is a vertical row of light detectors and
indicators (DI). The beam hits the detector which is at 1 meter height
(DI 1) as shown by its light switching on. Next, the lift is rising at
a great
velocity, and the light source is flashed on again. This time the DI at
one meter does not light, but one that is lower does, and the faster
the lift is rising, the lower the DI which is activated.
This experiment “proves” that light has mass.
I shall now do another thought experiment to prove that sound has mass
:-
Exp 2. Replace the light source with a sounder which can channel its
output within a narrow beam, and the target DIs are replaced with mono
directional microphones and indicators. When the lift is stationary,
the sound pulse hits the 1 meter height DI. When the lift is moving
however, the sound pulse does not hit the 1 meter high DI, but one
lower down the side of the lift. The faster the lift is moving, the
lower the DI, as proved by the appropriate light switching on.
This experiment "proves" that sound has mass.
We have here two experiments, but I have been very lax in setting out
the conditions of each. What were the conditions which Einstein (failed
to) set out in his experiment? The experiment with sound cannot be done
in a vacuum, it has to be done in air, but it can be done at varying
atmospheric pressures, and then we would discover that the mass of
sound varied in proportion to the pressure. The higher the pressure,
the less the downward movement of the sound pulse along the row of
microphones for a given lift velocity, therefore sound has less mass at
higher atmospheric pressures. It is actually of course, caused by sound
travelling faster in a higher pressure. One further point. Is the lift
an enclosed box, or is it a lattice work frame? If an enclosed box, the
air inside the lift is entrained, and would travel with the lift, and
the sound pulse would arrive at DI 1 no matter what the speed of the
lift. If it is a lattice work frame (is this implicitly assumed in
experiment 1?), the air in the lift is stationary with respect to the
ground, and the conditions of exp. 2 would prevail. In experiment 1, is
the air entrained with and therefore having the same velocity as the
lift, or stationary with respect to the ground? The exact argument used
for
experiment 2 holds good here also. Is there in fact any air present, or
is the experiment done in a vacuum? The conditions of the original
thought experiment are very ambiguous.
Now some may object to my saying "...is experiment 1 done in air or a
vacuum...", noting my disregard for the index of refraction, because a
vacuum cannot be entrained. My answer to this is that a pure vacuum
simply
does not exist. Space is full of matter, even intergalactic space. And
because
of that fact, I wish to ask a simple question, but one which will bring
howls of derision from some quarters. Can light travel through a pure
vacuum? That question was asked long ago, and because space was thought
to be a pure vacuum, the answer had to be yes. It demonstrably did so.
Light therefore had to be a particle phenomenon, and so came the
discussions
about wave versus particle, and wave/particle duality, and the photon
was born.
Light is a pure wave phenomenon, it has no existence of its own; it is
just like sound, a vibration of the atoms/molecules in the medium it is
travelling through. As the medium in intergalactic space is very
sparse, one atom per meter on average, this vibration can bridge that
gap. The mechanism by which that occurs? I am open to suggestions -
this is speculation. The fact that I do not know the answer to this key
question by no means invalidates my argument, scientists do not know
what gravity is, yet we are comfortable with equations which predict
its effect.
The fact that light is a wave answers Olber's paradox, and explains why
there are dark patches in the sky - the Coal Sack being perhaps the
most famous (if these patches were simply matter - ie dust, and
blocking out the light from the stars behind, they would have by now
warmed up and be re-radiating). There are regions of space which are so
rareified that light cannot cross them, and a dark area is created. The
density in these areas must be less than 1 atom per meter. If there are
many of these dark areas, they would cut off sufficient light to solve
Olber's
paradox. Olber's paradox is not solved as some claim, by light from
distant parts of the universe not having had time to reach us. This
implies the truth of the Big Bang theory, and not only that, but that
there was only one big bang.
At one time, we thought that the Earth was the centre of the
Universe. Then ditto the sun. Then we thought the sun was at the centre
of the (only) galaxy. We now know that our sun is an insignificant star
in an insignificant galaxy amongst billions (or an infinite number) of
others.
The Universe is infinite in size, and infinitely old, and within the
Universe there are big bangs occurring randomly in time and space. Step
far enough back to take a fresh look, and each one of these big bangs
looks like a galaxy, but each one is what we would call a universe -
what I call a quasi-universe. It makes no difference whether there is
enough matter (including dark matter) in each of these quasi-universes
to slow it's expansion and collapse it. On average, 50% will collapse
and 50% will expand forever, keeping the status quo. In this model of
the Universe, with quasi-universes rotating about a common centre,
light from approximately half of these quasi-universes will have had
time to reach us (assuming that at any one instant, 50% of those which
will collapse have collapsed, and are therefore going to be re-born,
and 50% of those which will not collapse have expanded to be too cold
and dim to be seen). As the Universe is infinite, that is still an
infinite number of quasi-universes. Light therefore has had an
infinite amount of time to reach us, but has not done so because the
density of matter in inter quasi-universal space is too low for light
to cross. Olber's paradox is therefore solved.
Return to menu.
9. THE TWIN PARADOX.
This is an update of the travelling versus the stay at home twin.
In the first preliminary step we take Earth and relocate it far into
intergalactic space. It will be far enough out such that gravity from
the nearest galaxy is a trillion times less than Earth's surface
gravity. The reason for doing this is firstly so that we don't need
to consider the gravity of surrounding stellar bodies, and secondly to
remove the motion of the Earth around the Sun and Milky Way from
consideration. Next we prevent the Earth from rotating. We do
this to avoid having to consider the SR/GR effects of the rotation
speed and the small amount of centrifugal force it provides.
Now to begin the story.
A rocket sits on the Earth's surface with a large supply of fuel.
Inside it is a room with living facilities and enough food and oxygen
to support an occupant for many months. It also contains an
accurate atomic clock. Beside the launch pad is an identically fitted
room. It contains a similar clock that has been synchronised with the
one aboard the rocket. There is also a third clock on the opposite side
of the Earth that is synchronised with the other two.
Two identical twins agree to take part in the experiment. Each will
spend the next several months either in the rocket or the Earth room,
but neither will know which. Prior to launch, they are both given a
sleeping pill. Each twin is then randomly assigned to
be moved into either the rocket or the stationary room.
The rocket lifts off. At first, very slowly so as not to apply much
acceleration. Then as it moves further from Earth and gravity
decreases, the rocket adjusts its acceleration to fill in what is
missing from Earth's gravity. This acceleration will be controlled so
that the gravity felt at all times will be exactly equal to 1G. That
is, the gravity measured by an on-board accelerometer (as the sum of
real plus artificial gravity) will measure the same as on Earth. Assume
that the rocket engine is silent and acceleration is smooth.
Shortly after launch, when the acceleration is a steady 1G, the twins
wake up. Neither of them know which room they are in. The rooms are
identical in layout and both experience what appears to be gravity. If
they drop something it will accelerate toward the floor at 9.81m/s2,
i.e. at 1G.
Now according to the Principle of Equivalence (also called the strong
equivalence principle), as proposed by Einstein and frequently
described by using falling elevators and rising rockets, the situation
inside the two rooms is essentially identical. That is, there is no
experiment you could devise that would allow either of the twins to
determine which room they are in. We will also assume the rooms are not
very tall. This is to prevent an occupant in the Earth-room from
measuring slightly less gravity near the ceiling.
According to the combined rules of SR and GR, will one of the clocks be
ahead of the other, and if so, what is the reason for selecting that
clock instead of the other?
The fact that the clocks are moving away from each other means there must be a velocity present, otherwise they would remain a fixed distance apart. Therefore, according to SR, time dilation should be occurring and the faster-moving clock should be running more slowly. But since the relative speed between the Earth and rocket is at all times exactly equal from both viewpoints, there appears to be no way of determining which is faster. As for GR, since the acceleration / gravity situation of both rooms is exactly equal at all times (other than the brief lift-off, when it was marginally more than 1G), according to the Equivalence Principle it would appear we are also unable to favour one clock over the other.
So we are left with a conundrum: either we find a way of
favouring one clock over the other or we agree that no time difference
accumulates between them. Now an objection might be that we have no way
of comparing the clocks without one of them stopping and reversing,
which would destroy the symmetry of the situation. And so the question
of which of them runs faster up until that point is somehow
hypothetical or meaningless. But this avoids the issue because the
question here is about which clock according to the theory of SR and
GR, runs slower. Unlike the Copenhagen Interpretation of quantum
mechanics, relativity does not depend on observers to determine the
reality of a situation. So the answer to this question won't depend on
the clocks ever being compared or not.
Still, this objection can be overcome and will be addressed in the
remainder of this essay
After travelling for 10 months, and using a simple classical mechanics
calculation, we could determine that the rocket is moving at 87% the
speed of light (relative to Earth, which is now relocated outside our
galaxy). At this speed we get a Lorentz factor of 2. This might mean
that either the rocket or Earth clock is running half the speed of the
other. These numbers however are not so important because we mainly
care about which clock is ahead of the other, and not by how much
(although we are also interested in that!). So let's just pick 10
months as an arbitrary duration and assume a rough Lorentz factor of 2
at that point. This factor will be sufficient to override minor
clock-drift errors, measurement errors, and brief periods where the
acceleration of the rocket is not 1G, such as the launch and rotation
(as described later). It should also cause noticeable differences in
what the twins remember about the duration of their journey, assuming
that one is running at half the speed of the other.
So after travelling for 10 months (according to the local clock) the
occupant aboard the rocket will take a sleeping pill. The same will
occur at
the Earth-room (according to their clock). Both twins will then sleep
for a while. The rocket engine will be stopped, allowing the craft
to drift freely in space with no acceleration. It will be gently
rotated 180 degrees to face the opposite direction, now pointing at
Earth. The engine will be started again, applying an acceleration
force of exactly 1G. Both twins will then wake up.
When the rocket-twin awakes, he notices no difference. Just as before,
he experiences what feels like a gravitational force of 1G toward the
floor. The Earth-twin experiences the same. The rocket is facing the
opposite direction and is now decelerating, but by all accounts
everything according to the Equivalence Principle is the same. There is
still no experiment either twin could perform to determine which is
experiencing gravity.
Therefore it would seem that according to GR, both clocks should still
be running at the same rate. And since the relative velocity is still
identical, that aspect never changes. The clocks' situation is
still symmetrical according to SR.
An objection here might be that there is a difference because the
clocks are experiencing gravity in opposite directions, therefore
the clock on the rocket will now be faster or slower (pick one!) than
the one on the Earth.
For those who raise this objection, refer instead to that third clock
placed on the other side of the Earth.
It is still in-synch with the first Earth clock and now experiencing
gravity in exactly the same direction as the rocket.
To continue the story, the deceleration process continues for the same
time as the original acceleration process (10 months), at which point
the rocket comes to rest relative to Earth. However the engine
doesn't stop. Instead it continues to apply exactly the same
amount of force. Deceleration becomes acceleration and the occupant
notices nothing unusual.
The acceleration continues for the next 10 months (according to the
local clock) until the rocket reaches (presumably) the original
rotation point. At this point (according to their own clocks), both
twins take the sleeping pill, the rocket is rotated 180 degrees, and
then
starts to decelerate while pointed away from Earth. Both twins awake
and notice nothing unusual in their gravity situation.
The rocket continues its deceleration in a perfect reverse of its
original departure, steadily coming to a stop relative to Earth, and
all the while carefully adjusting its acceleration to give an on-board
experience of 1G.
Just prior to landing, both twins take a sleeping pill and then wake up
after landing.
The rocket has now landed beside the replica Earth room. Neither twin
has yet to emerge, and neither still has any idea which one of them was
aboard the rocket.
Not that it matters. This story was never about the twins, it was about
the atomic clocks. The twins were just there to make it interesting and
to bring it into line with historical thought experiments such as
falling elevators and the Twins Paradox.
So to state the obvious question: allowing for minor
clock-drift
errors and the brief periods of launch, landing, and rotation, when the
clocks are compared side-by-side, which of them will have recorded more
time? And why not the other way around?
And while we are at it, which of the twins will be older?
This discussion of the twins' paradox can also be found on Bernard
Burchell's web site :- Alternativephysics
Return to menu.
10. EXPERIMENTAL EVIDENCE ON THE CONSTANCY OF THE VELOCITY OF LIGHT
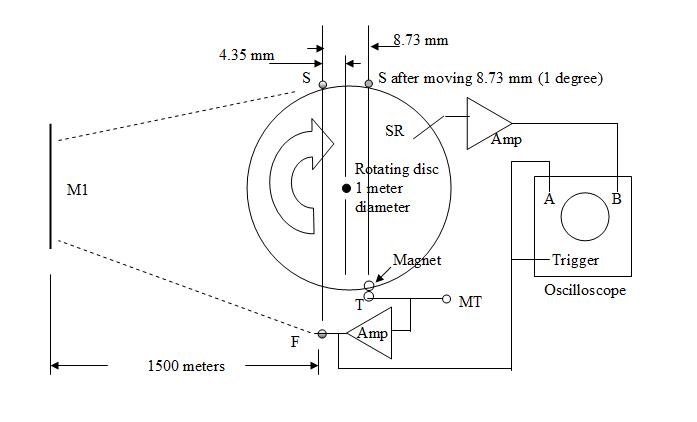
S light sensor
M1 mirror
(front silvered)
SR slip rings
F source of flash
MT
manual trigger
T
trigger
The disc has a light sensor S on its circumference, connected
electrically via slip rings SR to the amplifier and then to the
oscilloscope
input A. At 180 degrees round the disc from the sensor, there is a
trigger T (eg hall effect) which will after amplification trigger the
scope and flash the source F when activated. Before
assembling S and F on the disc, to find their switch
on delays (SOD), place them adjacent to each other - ie
touching,
and activate the manual trigger. Any delay in the rise time of A is due
to the SOD and the slew rate of the amp, which should be noted and
taken into account in later measurements when the disc is spinning.
With S and F back in place, and the disc stationary, set the disc so
the line S to F is perpendicular to the line from the mirror M to the
centre of
the disc. Activate the trigger T without moving the disc. Adjust the
trace position and the time base to bring the pulse on the A
trace (the trigger is activated when the pulse is emitted from
the
amp) to the left hand graticule line, so the pulse from S will show on
the B trace after about a 10 us delay, plus whatever is needed
for the lead length differences and the SODs of F and S). Move the disc
one degree so the flash has 8.73 mm farther to travel to reach the
sensor.
With the disc stationary at this new position, check the delay between
triggering the flash and its reception at the sensor. It should be
an extra 29.11 ps. This will be difficult to measure and will entail
careful use of the delayed and/or expanded time base.
Spin the disc at 21,600 rpm. This speed was chosen so the disc would
rotate 1 degree during the 10 us light travel time. The flash from F
takes 10 us to reach initial position of sensor S via
mirror M. In that time the disc has rotated 1 degree. 1 degree on the
circumference of a disc of 1 meter diameter is 8.73
mm, therefore the time for light to cross that extra distance
to
reach S is 29.11 ps. As the sensor on the disc moves cicumferencially,
while light travels linearly, there is a very slight discrepancy in the
distance travelled, but the error is negligible.
If the speed of light is with respect to the sensor (the observer) :-
The sensor is travelling (this is assuming a straight line distance,
but in fact it is circumferencial) away from the flash at 1,131.4 M/S,
but it will take the flash 10 us to reach S whatever the speed of S
(because S was 3,000 meters away from F at the time of the flash).
If the speed of light is with respect to its source or the medium :-
The sensor is travelling away from the flash at 1,131.4 M/S. The time
taken for light to cross the extra 8.73 mm is 29.11 ps, therefore
the flash takes 10.00002911us to reach S.
The 10 us has been adjusted out by the delayed time
base, so the scope time base can be adjusted to see the delay of
29.11 ps between the left hand graticule line and the start of the
trace.
In principle the distance F to S can be increased dramatically for
easier measurement of the time difference expected. If 2
mirrors
were to be placed parallel to
each other and as far apart as practicable, the flash could bounce from
one to the other many times, so increasing the path length without
unduly increasing the size of the apparatus. The greater the
distance F to S, the disc can be proportionally smaller/slower.
However, as the time F to S is larger, the delayed time base, which has
to
delay the signal to the scope by the same amount of time F to S, also
has to be larger, and may not be attainable. Also the greater the
distance F to S, the easier the discrepancy is to
measure, but the harder the apparatus is to set up, and more
importantly, to transport.
There is another way to make reading the results easier, but it involves a more in depth knowledge of electronics. Use an IC 555 in pulse mode to creat a pulse 95 uS in length. This pulse is triggered by the same trigger pulse which initiates the flash, but it is triggered by the trailing edge of the trigger pulse to allow the first flash through. This pulse is fed to the second input of the amplifier, and inhibits the next nine pulses, so there is a flash every 10 degrees of movement of the disc instead of 1 degree. The 29.11 pS delay now becomes 291.1 pS, which is much easier to read on the 'scope.
Problems.
1. Is there a scope fast enough to show a difference of 29 ps? Yes,
Tektronix CSA8200 .
2. Can a disc 1 meter in diameter be spun at 21,600 rpm and held steady
at
that speed? Yes, kevlar is strong and light enough to withstand the
stress.
3. The apparatus is not portable with a distance to the mirror of 1.5
Km.
Objections.
The flash will take 10.00002911 us to reach S due to the motion of the
disc. Relativists will say that this result is because the speed of
light is with respect to the air. This was not said of the MMX, which
"proved" that the speed of light was constant in a vacuum (?!).
Unfortunately, the experiment cannot be repeated in orbit, as the light
path length to the mirror, to make any difference measurable, is too
great at 1.5 Km.
Return to menu.
11. CONCLUSIONS.
The Equivalence Principle has been proven not hold for large masses, so
is therefore wrong.
Einstein’s definition of simultaneity, upon which he builds his theory
of time dilation, is wrong.
There is no contraction along the line of motion, it is simply a visual
effect.
The speed of light is not a constant, but is with respect to the medium
it is travelling through, even a very rarefied medium such as space.
Light probably cannot propagate through a pure vacuum. There are three
somewhat arbitrary speed bands for light in space. It is fastest in
inter-galactic space where the medium density is about one atom per
square meter on average. Next fastest is inter-stellar space where the
medium is about one atom per 10 square centimeters on average. Slowest
is
inter-planetary space where (our) medium is about one atom per square
centimeter on average. These speeds are all relative to that medium,
which can be seen to be the ether, and has an average velocity of zero
when taken over a large enough distance so that the currents cancel out.
A spaceship which carries it’s own means of propulsion - e.g. a rocket
motor, can travel faster than the speed of light. The light barrier, or
Luxon Wall as some writers have dubbed it, is non existent. A problem
which will make trans-light speeds difficult, but not impossible, is
that of the density of matter in space. At light speed, in
interplanetary space, the space ship will encounter on average one
atom per square centimeter of frontal area every 30 picoseconds.
Consider
the kinetic energy and friction on the hull.
There is no "Twin Paradox" due to velocity.
As the speed of light is not a constant, there is no time dilation
between moving (non accelerating) frames of reference. Absolute time
can be used. That is one of the constants in this universe - Time.
Return to menu.
12. APPENDIX
In chapter VI, Einstein has a man walking along in the carriage in the
direction of motion, and discusses the classical addition of
velocities. If w is the speed of the man with reference to the train,
and v is the speed of the train relative to the embankment, then W is
the speed of the man relative to the embankment W = v + w.
In chapter VII, he swaps the man for a light beam. Quote "It is obvious
that we can here apply the considerations of the previous section,
since the ray of light plays the part of the man walking along
relatively to the carriage."
However, quote "If a ray of light be sent along the embankment..."
notice that the 2 situations are different. The man in chapter VI is in
the carriage, while the ray of light in chapter VII is on the
embankment. "Let us enquire about the velocity of propagation of the
ray of light relative to the carriage... and we have w = c - v " If he
hadn't swapped IFRs, the velocity of propagation would have come out at
c. It was precisely because the answer was less than c, that SRT was
born, and all that it entails. This error also has a direct bearing on
the thought experiment in chapter IX. The man on the train "...is
hastening towards the beam of light..."
Another error is this :-
This error is to be found in his 1905 paper, presumably it was pointed
out to him as it is not present in his later book "Relativity - The
special And The General Theory". After establishing that time runs at
different rates in different IFRs, he goes on to show how to
synchronise clocks in IFR A and IFR B.
"We have so far defined only an ``A time'' and a ``B time.'' We have
not defined a common ``time'' for A and B, for the latter cannot be
defined at all unless we establish by definition that the ``time''
required by light to travel from A to B equals the ``time'' it requires
to travel from B to A.
Let a ray of light start at the ``A time'' tA from
A towards B, let it at the ``B time'' tB be reflected at B in the
direction of A, and arrive again at A at the ``A time'' t'A.
In accordance with definition the two clocks synchronize if
tB - tA = t'A - tB
At first glance this looks reasonable, but look closer. The sum above
is meaningless unless the clocks at A and at B are synchronized
already. If B is ticking at a different rate to A (which Einstein says
it is) the result is nonsense. "This equation does not define
synchronized clocks, but requires them" . Quote from "Relativity
Unraveled"
This error was brought to my attention by Hans Zweig.
I am indebted to my friend Hans J Zweig for his support in our ongoing
battle to unseat SRT. He has published a book called "Relativity
Unraveled", which I thoroughly recommend to anybody who has any
questions at all about SRT, or who simply thinks that it is wrong. A
preview of it is here :- http://www.relativityunraveled.net.
I include this link to professor Dingle's book, because anybody who has the slightest doubt (and in fact anybody who does not) about the truth of the Theory of Special Relativity should read it. I read it long ago, and re-read it recently. I was astounded by it - both times. It is even more relevant now than when professor Dingle wrote it in 1971. I urge you to read it with an open mind. Science at the Crossroads.
Return to menu.
Send email to the author :- carmam1536"at"gmail.com
You are visitor number :-